스토크스 변수

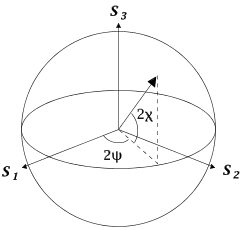
스토크스 변수는 (가시광선 등을 포함한) 전자기파의 편광 상태를 설명하기 위해 도입된 값이다. 이 변수들은 1852년 조지 가브리엘 스토크스에 의해, 결맞지 않거나 부분 편광된 광선에서 전체 광량 (Intensity, I), 편광도(Degree of polarization, p), 그리고 편광 타원의 모양변수 등에 대한 일반적인 설명을 간편하게 수학적으로 대체하기 위해 도입되었다. 스토크스 변수와 광량, 편광 타원의 매개변수들 사이의 관계는 다음의 관계식과 그림에 나타나 있다.

포앵카레 구면

${\begin{matrix}S_{0}&=&I\\S_{1}&=&Ip\cos 2\psi \cos 2\chi \\S_{2}&=&Ip\sin 2\psi \cos 2\chi \\S_{3}&=&Ip\sin 2\chi \end{matrix}}$

여기에서 $Ip$, $2\psi$, $2\chi$는 스토크스 변수 $S_{1}$, $S_{2}$, $S_{3}$를 3차원 공간상에 표현했을 때 편광 상태의 구면 좌표계 성분들이다. 위 식에서 $\psi$ 앞의 상수 2는 어떤 편광 타원이든 180°회전시 구분할 필요가 없음을 뜻하고, $\chi$ 앞의 2는 타원의 반축 길이가 90°회전과 연계되어 바뀜을 가리킨다. 네 스토크스 변수들은 각각 I, Q, U, V로 쓰이기도 한다.

스토크스 변수들이 주어지면 각각의 구면 좌표계 성분은 다음과 같은 식으로 정리할 수 있다.

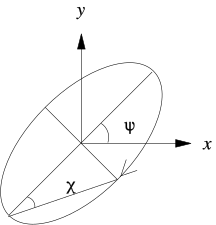
편광 타원

${\begin{matrix}I&=&S_{0}\\2\psi &=&\tan ^{-1}{\frac {S_{2}}{S_{1}}}\\2\chi &=&\tan ^{-1}{\frac {\cos 2\psi }{S_{1}}}\\p&=&{\frac {s3}{I\sin 2\chi }}\\\end{matrix}}$

스토크스 벡터

스토크스 변수들은 종종 스토크스 벡터라 불리는 벡터의 형태로 사용된다.

${\vec {S}}\ ={\begin{pmatrix}S_{0}\\S_{1}\\S_{2}\\S_{3}\end{pmatrix}}={\begin{pmatrix}I\\Q\\U\\V\end{pmatrix}}$

스토크스 벡터는 무편광(unpolarized), 부분편광(partially polarized), 또는 완전편광(totally polarized)된 빛의 공간을 생성(span)한다. 참고로, 존스 벡터는 완전편광된 빛의 공간만 생성할 뿐이지만 결맞은 빛의 문제를 해결하는 데에는 더 유용하기 때문에 널리 쓰인다. 사실 네 개의 스토크스 변수는 공간에서의 축요소(basis)로 쓸 수 있는 것도 아니지만, 측정하거나 계산하기 쉽기 때문에 선택한 것이다.

광학계의 편광 효율는 입사광의 스토크스 벡터 집합에 뮬러 행렬을 곱하면 빛이 광학계를 투과한 후의 스토크스 벡터를 구하면서 바로 확인할 수 있다.

예시

다음 예시는 일반적인 빛의 몇몇 편광 상태를 스토크스 벡터로 표현한 것이다.

편광형태	선형편광 (수평)	선형편광 (수직)	선형편광 (+45˚)	선형편광 (-45˚)
스토크스 벡터	${\begin{pmatrix}1\\1\\0\\0\end{pmatrix}}$	${\begin{pmatrix}1\\-1\\0\\0\end{pmatrix}}$	${\begin{pmatrix}1\\0\\1\\0\end{pmatrix}}$	${\begin{pmatrix}1\\0\\-1\\0\end{pmatrix}}$
편광형태	우원편광	좌원편광	무편광
스토크스 벡터	${\begin{pmatrix}1\\0\\0\\1\end{pmatrix}}$	${\begin{pmatrix}1\\0\\0\\-1\end{pmatrix}}$	${\begin{pmatrix}1\\0\\0\\0\end{pmatrix}}$

다른 방식의 설명

단색 평면파는 전파되는 방향의 벡터(propagation vector) ${\vec {k}}$와 축요소가 $({\hat {\epsilon }}_{1},{\hat {\epsilon }}_{2})$일 때 전기장의 복소수 진폭 $E_{1}$, $E_{2}$의 관계식으로 표현할 수 있다. 또한, 전파 벡터, 위상 $\phi$, (그리고 고정된 평면에서 전기장의 변화 곡선을 투영한) 편광 상태 $\Psi$의 관계식으로 표현할 수도 있다. 널리 알려진 편광 상태인 직선편광과 원편광은 가장 일반적인 타원편광의 특수한 경우라 할 수 있다.

일반적인 타원편광은 편광 타원의 반장축(半長軸; 타원의 장축 길이 절반) A와 반단축(半短軸; 타원의 단축 길이 절반) B인 타원이 x 축에서 $\theta$만큼 회전한 것으로 설명할 수 있다 (오른쪽 그림 참조). 스토크스 변수 I, Q, U, V는 실험적으로 편광 상태를 설명할 때 편리하게 사용되는데, 각 변수들이 측정된 광도의 합이나 차와 바로 연관되기 때문이다. 다음 그래프들은 특수한 경우 스토크스 변수들의 예이다.

정의

스토크스 변수는 다음과 같이 정의된다.

${\begin{matrix}I&\ {\stackrel {\mathrm {def} }{=}}\ &|E_{x}|^{2}+|E_{y}|^{2},\\&=&|E_{a}|^{2}+|E_{b}|^{2},\\&=&|E_{l}|^{2}+|E_{r}|^{2},\\Q&\ {\stackrel {\mathrm {def} }{=}}\ &|E_{x}|^{2}-|E_{y}|^{2},\\U&\ {\stackrel {\mathrm {def} }{=}}\ &|E_{a}|^{2}-|E_{b}|^{2},\\V&\ {\stackrel {\mathrm {def} }{=}}\ &|E_{l}|^{2}-|E_{r}|^{2},\end{matrix}}$

여기서 밑에 쓰인 문자들은 각각 세 축요소를 뜻한다. 데카르트 좌표에서 (${\hat {x}},{\hat {y}}$), 데카르드 좌표계를 45°회전시킨 경우의 (${\hat {a}},{\hat {b}}$), 원통 좌표계에서 (${\hat {l}},{\hat {r}}$). 원통 좌표계에서 ${\hat {l}}=({\hat {x}}+i{\hat {y}})/{\sqrt {2}}$이다. 다음 그림은 스토크스 변수의 부호가 편광 타원의 반장축 방향과 회전방향에 따라 어떻게 바뀌는지 보여준다.

고정된 축에 대한 표현

고정된 (${\hat {x}},{\hat {y}}$)에 대해, 스토크스 변수는 다음과 같다.

${\begin{matrix}I&=&|E_{x}|^{2}+|E_{y}|^{2},\\Q&=&|E_{x}|^{2}-|E_{y}|^{2},\\U&=&2{\mbox{Re}}(E_{x}^{*}E_{y}),\\V&=&2{\mbox{Im}}(E_{x}^{*}E_{y}),\\\end{matrix}}$

반면, $({\hat {a}},{\hat {b}})$에 대해선,

${\begin{matrix}I&=&|E_{a}|^{2}+|E_{b}|^{2},\\Q&=&-2{\mbox{Re}}(E_{a}^{*}E_{b}),\\U&=&|E_{a}|^{2}-|E_{b}|^{2},\\V&=&2{\mbox{Im}}(E_{a}^{*}E_{b}).\\\end{matrix}}$

이고, $({\hat {l}},{\hat {r}})$에 대해선

${\begin{matrix}I&=&|E_{l}|^{2}+|E_{r}|^{2},\\Q&=&2{\mbox{Re}}(E_{l}^{*}E_{r}),\\U&=&-2{\mbox{Im}}(E_{l}^{*}E_{r}),\\V&=&|E_{l}|^{2}-|E_{r}|^{2}.\\\end{matrix}}$

이 된다.

속성

순수한 단색의 결맞은 빛(monochromatic coherent light)의 경우엔

${\begin{matrix}Q^{2}+U^{2}+V^{2}=I^{2},\end{matrix}}$

이지만, 보통의 백색광(결맞지 않은)의 경우에 스토크스 변수는 평균값으로 정의되고, 위의 등식은 다음과 같은 부등식이 된다.

${\begin{matrix}Q^{2}+U^{2}+V^{2}\leq I^{2}.\end{matrix}}$

그러나, 여기에서 총 편광량(total polarized intensity) $I_{p}$를 정의해서

${\begin{matrix}Q^{2}+U^{2}+V^{2}=I_{p}^{2},\end{matrix}}$

로 쓸 수 있고, $I_{p}/I$는 전체 편광 비율이 된다.

선형편광시 복소 광량을 다음과 같이 정의해보자.

${\begin{matrix}L&\ {\stackrel {\mathrm {def} }{=}}\ &|L|e^{i2\theta }\\&\ {\stackrel {\mathrm {def} }{=}}\ &Q+iU.\\\end{matrix}}$

편광 타원에서 $\theta \rightarrow \theta +\theta '$로 회전했을 때, I 와 V는 불변이지만,

${\begin{matrix}L&\rightarrow &e^{i2\theta '}L,\\Q&\rightarrow &{\mbox{Re}}\left(e^{i2\theta '}L\right),\\U&\rightarrow &{\mbox{Im}}\left(e^{i2\theta '}L\right).\\\end{matrix}}$

이 되어, 스토크수 변수들의 다음과 같은 경향성을 추론할 수 있다.

${\begin{matrix}I&\geq &0,\\V&\in &\mathbb {R} ,\\L&\in &\mathbb {C} ,\\\end{matrix}}$

여기서 I는 전체 광량을 의미하고, $|V|$, $|L|$은 각각 원편광, 선형편광된 광량을 뜻한다. 이때 전체 편광된 광량 $I_{p}={\sqrt {L^{2}+V^{2}}}$이고, 타원축의 방향과 회전은 다음과 같이 주어지게 된다.

${\begin{matrix}\theta &=&{\frac {1}{2}}\arg(L),\\h&=&\operatorname {sgn}(V).\\\end{matrix}}$

여기서 $Q={\mbox{Re}}(L)$이고 $U={\mbox{Im}}(L)$이기 때문에,

${\begin{matrix}|L|&=&{\sqrt {Q^{2}+U^{2}}},\\\theta &=&{\frac {1}{2}}\tan ^{-1}(U/Q).\\\end{matrix}}$

이 된다.

편광 타원과의 관계

편광 타원에서 매개변수들은 스토크스 변수인

${\begin{matrix}I_{p}&=&A^{2}+B^{2},\\Q&=&(A^{2}-B^{2})\cos(2\theta ),\\U&=&(A^{2}-B^{2})\sin(2\theta ),\\V&=&2ABh.\\\end{matrix}}$

를 가리키며, 위 식을 통해

${\begin{matrix}A&=&{\sqrt {{\frac {1}{2}}(I_{p}+|L|)}}\\B&=&{\sqrt {{\frac {1}{2}}(I_{p}-|L|)}}\\\theta &=&{\frac {1}{2}}\arg(L)\\h&=&\operatorname {sgn}(V).\\\end{matrix}}$

임을 알 수 있다.

같이 보기

• 뮬러 행렬
• 존스 행렬
• 편광